分解质因数 引入 给定一个正整数 非平凡因数 。
考虑朴素算法,因数是成对分布的,
当
朴素算法 最简单的算法即为从
我们能够证明 result 中的所有元素均为 N 的素因数。
证明 result 中均为 首先证明元素均为 N % i == 0 满足时,result 发生变化:储存 result 若在 push N
其次证明 result 中均为素数。我们假设存在一个在 result 中的合数 while(N % k1 == 0) N /= k1,即让 N 没有了素因子 N 和
值得指出的是,如果开始已经打了一个素数表的话,时间复杂度将从 筛法 处查阅更多打表的信息。
例题:CF 1445C
Pollard Rho 算法 引入 而下面复杂度复杂度更低的 Pollard-Rho 算法是一种用于快速分解非平凡因数的算法(注意 !非平凡因子不是素因子)。而在此之前需要先引入生日悖论。
生日悖论 不考虑出生年份(假设每年都是 365 天),问:一个房间中至少多少人,才能使其中两个人生日相同的概率达到
解:假设一年有
设
至少有两个人生日相同的概率为
由不等式
因此
将
当
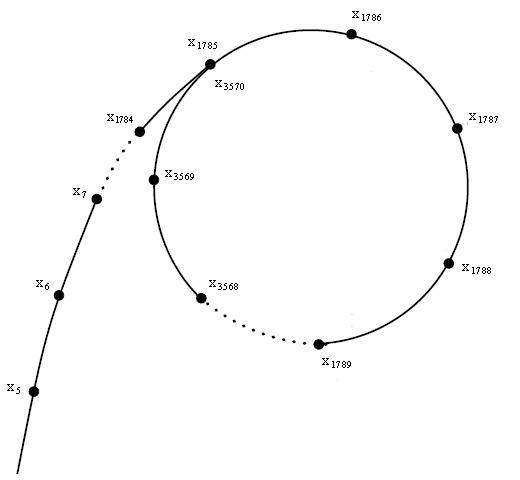
考虑一个问题,设置一个数据
利用最大公约数求出一个约数
我们通过
举个例子,设
可以发现数据在
选择
证明 若
同理,
根据生日悖论,生成的序列中不同值的数量约为
将
因此,我们可以期望在
同理,任何满足
一般选择
性质 我们期望枚举
下面介绍两种实现算法,两种算法都可以在
实现 Floyd 判环 假设两个人在赛跑,A 的速度快,B 的速度慢,经过一定时间后,A 一定会和 B 相遇,且相遇时 A 跑过的总距离减去 B 跑过的总距离一定是圈长的 n 倍。
设
我们每次令
基于 Floyd 判环的 Pollard-Rho 算法 C++ Python
1
2
3
4
5
6
7
8
9
10
11
12 ll Pollard_Rho ( ll N ) {
ll c = rand () % ( N - 1 ) + 1 ;
ll t = f ( 0 , c , N );
ll r = f ( f ( 0 , c , N ), c , N );
while ( t != r ) {
ll d = gcd ( abs ( t - r ), N );
if ( d > 1 ) return d ;
t = f ( t , c , N );
r = f ( f ( r , c , N ), c , N );
}
return N ;
}
1
2
3
4
5
6
7
8
9
10
11
12 import random
def Pollard_Rho ( N ):
c = random . randint ( 1 , N - 1 )
t = f ( 0 , c , N )
r = f ( f ( 0 , c , N ), c , N )
while t != r :
d = gcd ( abs ( t - r ), N )
if d > 1 :
return d
t = f ( t , c , N )
r = f ( f ( r , c , N ), c , N )
return N
倍增优化 使用 欧几里得算法 有
我们每过一段时间将这些差值进行
注意到在环上更容易分解出因数,我们可以先迭代一定的次数。
实现 C++ Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 ll Pollard_Rho ( ll x ) {
ll t = 0 ;
ll c = rand () % ( x - 1 ) + 1 ;
// 加速算法,这一步可以省略
for ( int i = 1 ; i < 1145 ; ++ i ) t = f ( t , c , x );
ll s = t ;
int step = 0 , goal = 1 ;
ll val = 1 ;
for ( goal = 1 ;; goal <<= 1 , s = t , val = 1 ) {
for ( step = 1 ; step <= goal ; ++ step ) {
t = f ( t , c , x );
val = val * abs ( t - s ) % x ;
// 如果 val 为 0,退出重新分解
if ( ! val ) return x ;
if ( step % 127 == 0 ) {
ll d = gcd ( val , x );
if ( d > 1 ) return d ;
}
}
ll d = gcd ( val , x );
if ( d > 1 ) return d ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 from random import randint
from math import gcd
def Pollard_Rho ( x ):
c = randint ( 1 , x - 1 )
s = t = f ( 0 , c , x )
goal = val = 1
while True :
for step in range ( 1 , goal + 1 ):
t = f ( t , c , x )
val = val * abs ( t - s ) % x
if val == 0 :
return x #如果 val 为 0,退出重新分解
if step % 127 == 0 :
d = gcd ( val , x )
if d > 1 :
return d
d = gcd ( val , x )
if d > 1 :
return d
s = t
goal <<= 1
val = 1
例题:P4718【模板】Pollard-Rho 算法
对于一个数 Miller Rabin 算法 判断是否为素数,如果是就可以直接返回了,否则用 Pollard-Rho 算法找一个因子
实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88 #include <bits/stdc++.h>
using namespace std ;
typedef long long ll ;
int t ;
long long max_factor , n ;
long long gcd ( long long a , long long b ) {
if ( b == 0 ) return a ;
return gcd ( b , a % b );
}
long long quick_pow ( long long x , long long p , long long mod ) { // 快速幂
long long ans = 1 ;
while ( p ) {
if ( p & 1 ) ans = ( __int128 ) ans * x % mod ;
x = ( __int128 ) x * x % mod ;
p >>= 1 ;
}
return ans ;
}
bool Miller_Rabin ( long long p ) { // 判断素数
if ( p < 2 ) return 0 ;
if ( p == 2 ) return 1 ;
if ( p == 3 ) return 1 ;
long long d = p - 1 , r = 0 ;
while ( ! ( d & 1 )) ++ r , d >>= 1 ; // 将d处理为奇数
for ( long long k = 0 ; k < 10 ; ++ k ) {
long long a = rand () % ( p - 2 ) + 2 ;
long long x = quick_pow ( a , d , p );
if ( x == 1 || x == p - 1 ) continue ;
for ( int i = 0 ; i < r - 1 ; ++ i ) {
x = ( __int128 ) x * x % p ;
if ( x == p - 1 ) break ;
}
if ( x != p - 1 ) return 0 ;
}
return 1 ;
}
long long Pollard_Rho ( long long x ) {
long long s = 0 , t = 0 ;
long long c = ( long long ) rand () % ( x - 1 ) + 1 ;
int step = 0 , goal = 1 ;
long long val = 1 ;
for ( goal = 1 ;; goal *= 2 , s = t , val = 1 ) { // 倍增优化
for ( step = 1 ; step <= goal ; ++ step ) {
t = (( __int128 ) t * t + c ) % x ;
val = ( __int128 ) val * abs ( t - s ) % x ;
if (( step % 127 ) == 0 ) {
long long d = gcd ( val , x );
if ( d > 1 ) return d ;
}
}
long long d = gcd ( val , x );
if ( d > 1 ) return d ;
}
}
void fac ( long long x ) {
if ( x <= max_factor || x < 2 ) return ;
if ( Miller_Rabin ( x )) { // 如果x为质数
max_factor = max ( max_factor , x ); // 更新答案
return ;
}
long long p = x ;
while ( p >= x ) p = Pollard_Rho ( x ); // 使用该算法
while (( x % p ) == 0 ) x /= p ;
fac ( x ), fac ( p ); // 继续向下分解x和p
}
int main () {
scanf ( "%d" , & t );
while ( t -- ) {
srand (( unsigned ) time ( NULL ));
max_factor = 0 ;
scanf ( "%lld" , & n );
fac ( n );
if ( max_factor == n ) // 最大的质因数即自己
printf ( "Prime \n " );
else
printf ( "%lld \n " , max_factor );
}
return 0 ;
}
参考资料与链接 2024/3/27 13:40:06 ,更新历史 在 GitHub 上编辑此页! iamtwz , 2740365712 , 383494 , Backl1ght , Bubbleioa , CCXXXI , Enter-tainer , GoodCoder666 , Great-designer , Ir1d , kenlig , leoleoasd , megakite , Menci , PeterlitsZo , Saisyc , ShaoChenHeng , shawlleyw , shuzhouliu , StudyingFather , TianKong-y , Tiphereth-A , usamoi , Xeonacid , xyf007 CC BY-SA 4.0 和 SATA